ch6树与二叉树

发表于 | 更新于: | 分类于 |
字数统计: 2.7k 字 | 阅读时长 ≈ 10 分钟
cover

来自离散数学和数据结构的合力打击，麻了。

6.1 树的概念与定义

a

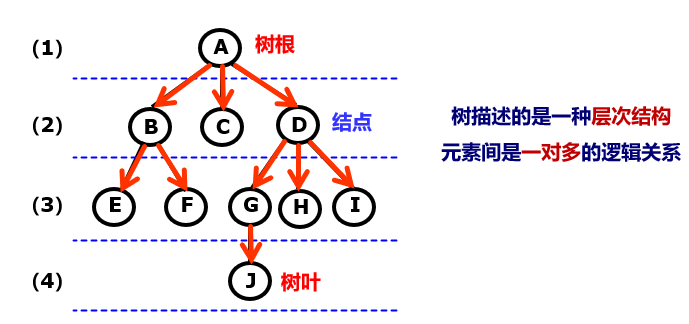
  • 树（Tree）：是定义在一对多关系上的层次化数据结构

  • 树的定义：树是n（n≥0）个结点的有限集合T，其中：

    1. 有且仅有一个特定的结点，称为树的根（root），它没有直接前驱，但有零个或多个直接后继。
    2. 当n>1时，其余结点可分为m个互不相交的有限集 T1, T2,……Tm，
    3. 其中Ti又是一棵树，称为根root的子树（subtree）。

b

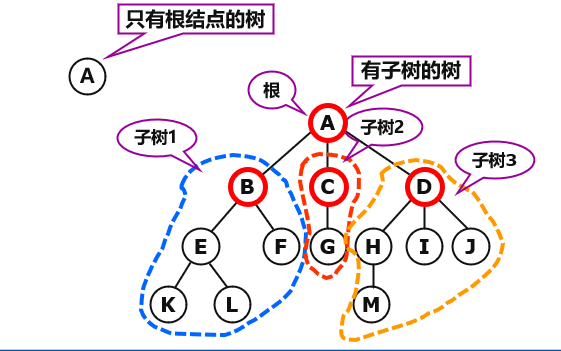
6.1.1、树的（逻辑）表示

  • 文氏图

每个节点都包含它所有的子孙节点，用圈框起来

  • 凹入表示法

c

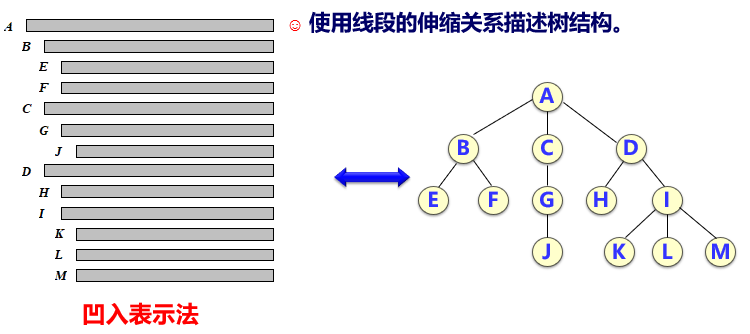
  • 括号表示法

类似于我们之前描述广义表时的表达式，上面的树化为括号表达式为：A(B(E，F)，C(G(J))，D(H，I(K，L，M)))

6.1.2、树的相关术语

这里就重点说一下几个易混易错的点：

d

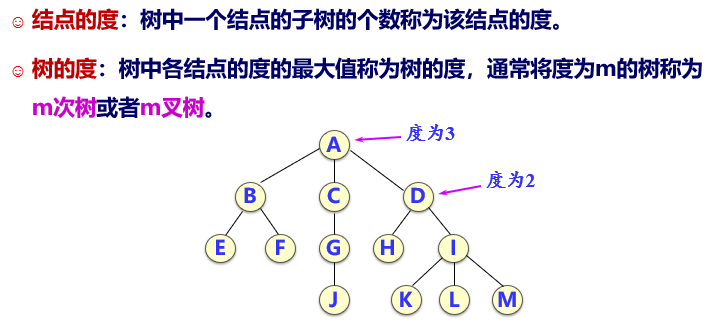
这里主要注意结点的度定义问题： 是连接子树的个数，不要把头上那根算上了

上图应为 三叉树

☺分支结点（非终端结点）：度不为零的结点。

☺叶结点（终端结点）：度为零的结点。

☺度为 1 的结点称为单分支结点；度为 2 的结点称为双分支结点，依此类推。

e

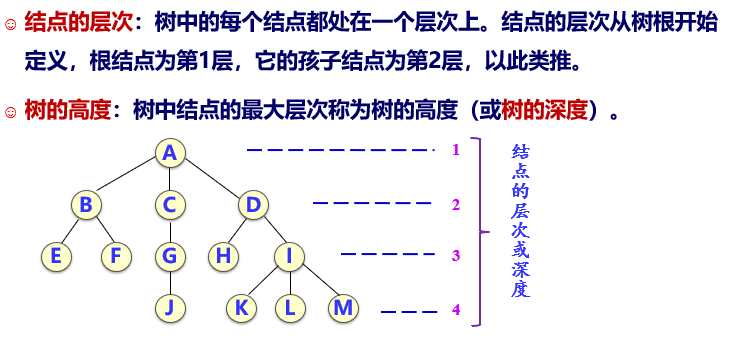
前辈 ：只要层号更小，都可以称为前辈

后辈 ：只要层号更大，都可以称为后辈

6.1.3、树的同构

f

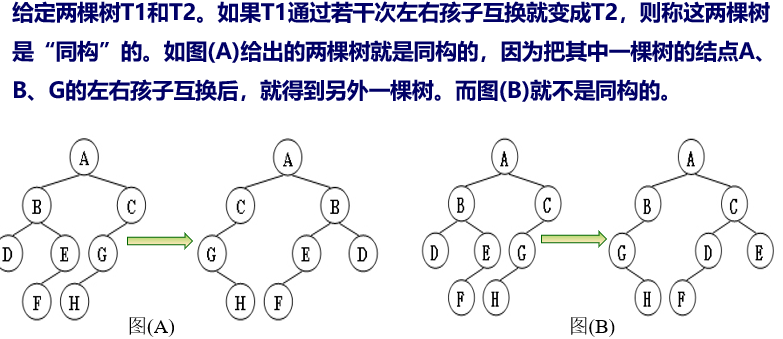
反正扭来扭去完全没问题，不过只要你敢伤筋动骨砍了某条连接边，就不再是同构了

6.1.4 、有序树和无序树

有序树的定义：若将树中每个结点的各子树看成是 从左到右有次序 的(即不能互换)，则称该树为 **有序树(Ordered Tree)**。
无序树的定义：若将树中每个结点的各子树 从左到右是没有次序 的(即可以互换)，则称该树为 无序树。

线性结构 树结构
第一个数据元素 无前驱 根结点 无双亲
最后一个数据元素 无后继 叶结点 无孩子
其它数据元素 一个前驱；一个后继 其它结点 一个双亲；多个孩子
元素之间的逻辑关系 一对一 结点之间的逻辑关系 一对多

6.2、二叉树

☺二叉树是一种简单而重要的树结构。

☺适合于计算机处理，任何树都可以转换为二叉树。

☺二叉树是重点研究对象。

6.2.1、二叉树的定义

  • 定义：我们把满足以下两个条件的树型结构叫做二叉树（Binary Tree）：
    （1）每个结点的度都不大于2；
    （2）每个结点的孩子结点次序不能任意颠倒。
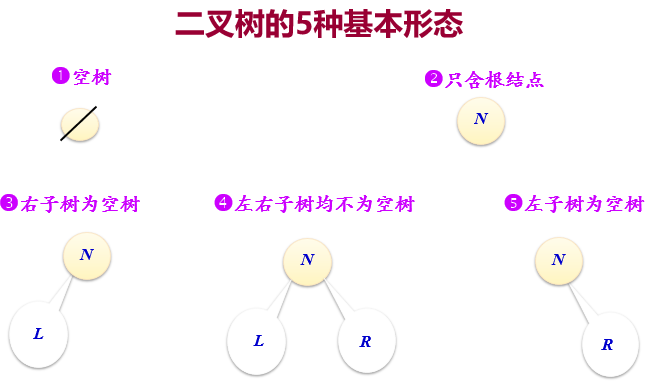
  • 一个二叉树的每个结点可能含有0、1或2个孩子，且每个孩子有左右之分。

g

6.2.2、二叉树的性质

证明略。

  • 性质1：在二叉树的第 i 层上至多有 2i - 1个结点( i ≥1)
  • 性质2：深度为 k 的二叉树至多有 2k - 1 个结点（k ≥1）
  • 性质3：对任意一棵二叉树T，若终端结点数为n0，而其度数为2的结点数为n2，则：
    n0= n2+1

满二叉树与完全二叉树：

这俩完全两个东西，注意区分：

满二叉树：深度为 k 且有 2k-1个结点的二叉树。在满二叉树中，每层结点都是满的，即每层结点都具有最大结点数。

满二叉树的排序方式简单粗暴，一层层从左往右数就行了

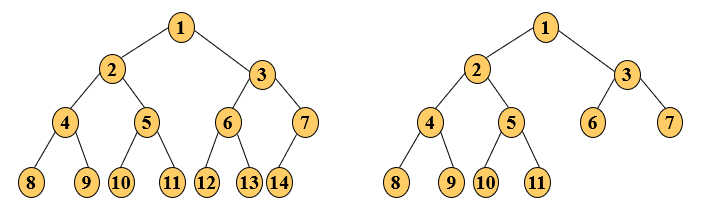
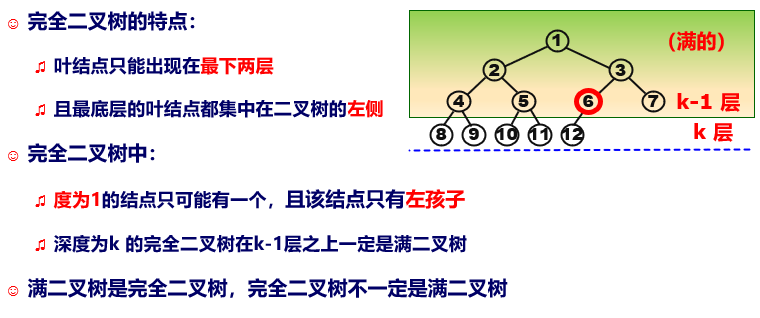
完全二叉树：对一棵具有 n 个结点的二叉树 T 按层序编号，如果编号为 i（1≤ i ≤ n）的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中的位置完全相同，则称 T 为完全二叉树。

h

i

  • 性质4：具有n个结点的完全二叉树的深度为：

$$
\lfloor log_{2}n\rfloor +1
$$

  • 性质5：对于具有 n 个结点的完全二叉树，如果按照从上到下和从左到右的顺序对二叉树中的所有结点从1开始顺序编号，则对于任意的序号为 i 的结点有：

① 若 i = 1, 则 i 无双亲结点
若 i >1, 则 i 的双亲结点为 i /2 向下取整
② 若 2i > n, 则 i 无左孩子
若 2i≤n, 则 i 结点的左孩子结点为 2i
③ 若 2i +1 > n ,则 i 无右孩子
若 2i +1≤n, 则 i 的右孩子结点为 2i+1

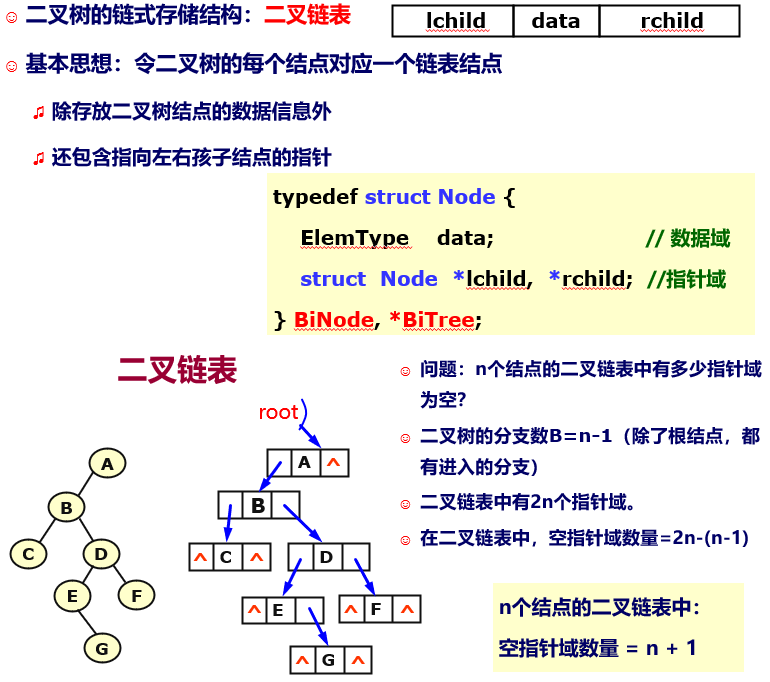
6.2.3、二叉树的存储结构

  • 二叉树的结构是非线性的，每一结点最多可有两个后继。

  • 二叉树的存储结构有两种：

    顺序存储结构：

    j

    若深度为 K ，则需要 2k - 1 个存储单元，因此很容易造成空间浪费。

    链式存储结构：

k

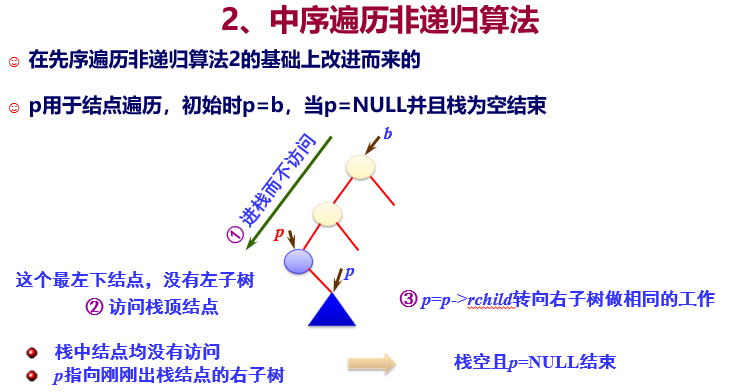
6.3、二叉树的遍历

  • 二叉树的遍历：
    指按一定规律对二叉树中的每个结点进行访问且仅访问一次。
    即：采用一定的方法得到树中所有结点的一个线性排列
  • 遍历是二叉树最基本的运算，是二叉树中其他运算的基础

我们一般把左子树、右子树、根节点分别标为 L、R、D，并且按访问他们的顺序不同将遍历方式分成 LDR、DLR 等不同的类型；其中，前序遍历、中序遍历、后序遍历 是我们现在要讨论的重点。

Q ：这三种方式命名的原则？

A ：其中，前、中、后是针对根节点而言，先访问根节点就叫做先序…… L 与 R 的顺序永远是 L 在前（对这三种来说）

Q ：访问方式？

A ：其实它的操作有一定的 递归性，对于每个根节点而言，在进行访问时访问到了左/右子树，则对其梅开二度，进行同类型的遍历

例：先序遍历某二叉树，若二叉树为空，则空操作，否则依次执行如下操作：
（1）访问根结点；
（2）按先序遍历左子树；
（3）按先序遍历右子树。

6.3.1、遍历算法应用

二叉树中的结点

1
2
3
4
5
6
7
8
/* 先序遍历输出二叉树结点, root为指向二叉树根结点的指针 */
void  PreOrder(BiTree root) {
    if (root!=NULL) {
        printf ("%c  ", root ->data);		/* 输出根结点 */
        PreOrder(root ->LChild); 	/* 先序遍历左子树 */
        PreOrder(root ->RChild); 	/* 先序遍历右子树 */
    }
}

好了，其实只需要这一个就够了。只要明白了怎么利用递归的方法遍历树，那么教材中该小节部分问题无非就是加计数器或者加判断的事了，比如：

1
2
if (root ->LChild==NULL && root ->RChild==NULL)
            LeafCount++;

这里用左孩子右孩子都为空判断是叶节点，再用 LeafCount 计数（全局变量）。

还有一种算法 b，是将其作为函数返回值（内部变量），再递归返回。

1
2
3
4
5
6
7
8
9
10
11
12
/*后续遍历：采用分治算法，如果是空树，返回0；如果只有一个结点，返回1；
     否则为左右子树的叶子结点数之和 */
int leaf_b(BiTree root) {
    int LeafCount;
    if(root==NULL)	
        LeafCount =0;
    else if((root->LChild==NULL)&&(root->RChild==NULL))
        LeafCount =1;
    else 		/* 叶子数为左右子树的叶子数目之和 */
        LeafCount = leaf_b(root->LChild) + leaf_b(root->RChild); 
    return LeafCount;
}

建立二叉链表方式存储的二叉树

l

1
2
3
4
5
6
7
8
9
10
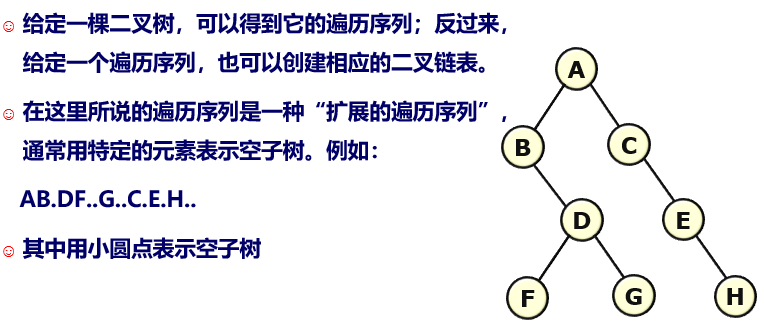
11
void CreateBiTree(BiTree *bt) {
    char ch;
    ch = getchar();
    if(ch=='.') *bt=NULL;
    else {
        *bt=(BiTree)malloc(sizeof(BiTNode)); 	//生成一个新结点
        (*bt)->data=ch;
        CreateBiTree(&((*bt)->LChild)); 		//生成左子树
        CreateBiTree(&((*bt)->RChild));		//生成右子树
    }
}

求二叉树高度

m

1
2
3
4
5
6
7
8
9
10
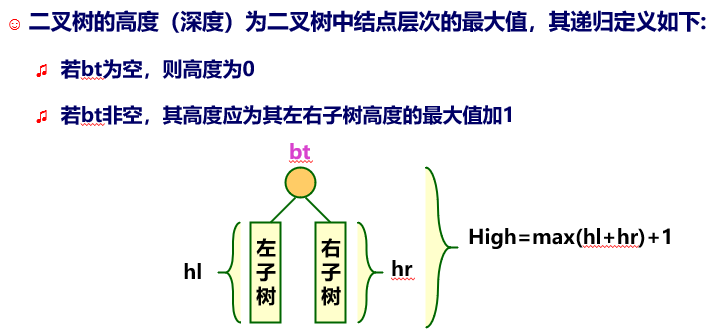
int PostTreeDepth(BiTree bt) {   /* 后序遍历求二叉树的高度递归算法 */
    int hl,hr,max;
    if(bt!=NULL) {
        hl=PostTreeDepth(bt->LChild); 	/* 求左子树的深度 */
        hr=PostTreeDepth(bt->RChild); 	/* 求右子树的深度 */
        max=hl>hr?hl:hr; 				/* 得到左、右子树深度较大者*/
        return(max+1); 				/* 返回树的深度 */
    }
    else return(0);                             /* 如果是空树，则返回0 */
}

或者使用 全局变量：

1
2
3
4
5
6
7
8
9
10
/* 前序遍历求二叉树bt高度的递归算法，h为bt指向结点所在层次，初值为1*/
/*depth为当前求得的最大层次，为全局变量，调用前初值为0 */
void PreTreeDepth(BiTree bt, int h) {
    if(bt!=NULL) {
        if(h>depth) 
            depth = h;		/*如果该结点层次值大于depth，更新depth的值*/
        PreTreeDepth(bt->Lchild, h+1);	/* 遍历左子树 */
        PreTreeDepth(bt->Rchild, h+1);	/* 遍历右子树 */
    }
}

6.3.2、递归消除

消除递归的一个办法就是用循环去替代它，但是在大量复杂的情况下，递归的问题无法直接转换成循环。所以我们这里的解决方案是用队列和栈来消除递归。

  • 可以用队列消除递归。
  • 可采用工作栈消除递归。工作栈提供一种控制结构：
    当递归算法进层时需要将信息保留；
    当递归算法出层时需要从栈区退出信息。

基于队列：

n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void LevelOrder(BiTree bt){
    BiTree Queue[MAXNODE];	/*定义队列*/
    int front, rear;
    if (bt==NULL) return; 		/*空二叉树，遍历结束*/
    front=0; rear=0;
    Queue[rear]=bt;			/*根结点入队列*/
    rear++;
    while((rear!=front){ 		/*队列不空，继续遍历，否则，遍历结束*/
        visit(Queue[front]->data); 	/*访问刚出队的元素*/
        if (queue[front]->lchild!=NULL) {	/*如果有左孩子，左孩子入队*/
            Queue[rear]=Queue[front]->lchild;
            rear++;
        }
        if (queue[front]->rchild!=NULL){	/*如果有右孩子，右孩子入队*/
            Queue[rear]=Queue[front]->rchild;
            rear++;
        }
        front++;  /*出队*/
    }
}

基于栈：

o

先序遍历非递归算法1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void PreOrder1(BiTNode *b) {
       BiTNode *p;
       SqStack *st;				//定义栈指针st
       InitStack(st);			//初始化栈st
       if (b!=NULL) {
	Push(st，b);			//根结点进栈
	while (!StackEmpty(st)) { 	//栈不为空时循环
	        Pop(st，p);			//退栈结点p并访问它
	        printf("%c "，p->data);
	        if (p->rchild!=NULL)	//有右孩子时将其进栈
		  Push(st，p->rchild);
	        if (p->lchild!=NULL)	//有左孩子时将其进栈
		   Push(st，p->lchild);
	}
	printf("\n");
       }
       DestroyStack(st);			//销毁栈
}

先序遍历非递归算法2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void PreOrder2(BiTNode *b){
    BiTNode *p;  SqStack *st;	//定义一个顺序栈指针st
    InitStack(st);			//初始化栈st
    p=b;
    while (!StackEmpty(st) || p!=NULL) {
        while (p!=NULL) { //访问结点p及其所有左下结点并进栈
            printf("%c "，p->data);	//访问结点p
            Push(st，p);		//结点p进栈
            p=p->lchild;		//移动到左孩子
        }
        //以下考虑栈顶结点
        if (!StackEmpty(st)) {	//若栈不空
            Pop(st，p);		//出栈结点p
            p=p->rchild;		//转向处理其右子树
        }
    }
    printf("\n");
    DestroyStack(st);		//销毁栈
}

p

q