相当不妙……马上就要期末考试了……我还有一堆事情,总之先搞一下总结。
上一单元总结:*ch4串 | PICOF’s blog*
5.1、数组的定义和运算
1、定义:
☺数组是一种数据类型。
☺从 逻辑结构 上看,数组可以看成是一般 线性表 的扩充。
☺二维数组可以看成是线性表的线性表。(就是把多个不同子线性表理解成元素放入大线性表中)

按照上面的逻辑,我们可以向 N 维度不断类推,即 N 维数组是数据元素为 N-1 维数组的线性表。
2、运算:
☺ 数组是一组有固定个数的元素的集合。
☺ 对数组的 操作 不象对线性表的操作那样,可以在表中任意一个合法的位置插入或删除一个元素。
☺ 对于数组的操作一般只有两类:
♫ 获得特定位置的元素值;
♫ 修改特定位置的元素值。
这里的运算实质上就牵扯到存放数据的地址计算问题了。
3、数组的抽象数据类型定义:


5.2、数组的顺序存储与实现:
数组不像链表一样,一般来说数组的基本操作是不会涉及结构的改变的(一般不会涉及插入、删除等链表类的操作,不涉及移动元素操作)。因此对于数组来说,顺序存储才是最合适的存储方法。

注:上图默认数组元素由 1 开始计数
☺二维数组的顺序存储结构有两种:
♫ 一种是按行序存储,如高级语言 C、BASIC、COBOL 和 PASCAL 语言都是以行序为主。
♫ 另一种是按列序存储,如高级语言中的 FORTRAN 语言就是以列序为主。
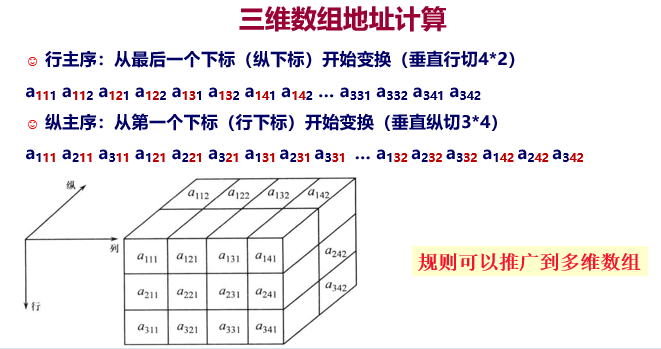
n维数组地址计算:
第一维主序:
LOC (j1, j2, … , jn ) = LOC (1, 1, … , 1) +
[ b2*b3*…*bn*(j1 - 1) + b3*b4*…*bn*(j2 - 1) + … + bn*(jn-1 - 1)+ (jn - 1) ] * size
5.3 特殊矩阵的压缩存储
☺在高级程序设计语言里面,矩阵通常采用二维数组表示。
☺特殊矩阵可采用 压缩存储 的方式
♫ 元素分布 有规律的矩阵,按规律实现压缩储存
♫ 非零元素少 的稀疏矩阵,采用 存非零元素 实现压缩存储
5.3.1、分布规律的特殊矩阵
1、三角矩阵:
☺ 三角矩阵( n阶矩阵)
- 下三角矩阵:若当 i < j 时,有aij=0
- 上三角矩阵:若当 i > j 时,有aij=0
- 对称矩阵:若矩阵中的所有元素均满足 aij = aji


2、带状矩阵:

☺ 三对角带状矩阵的压缩存储,以 行序为主序 进行存储,并且只存储非零元素
☺ 确定存储该矩阵所需的一维向量空间的大小
♫ 除第一行和最后一行只有两个元素外,其余各行均有 3 个非零元素。由此可得到一维向量所需的空间大小为:**3n-2 **
☺确定非零元素在一维数组空间中的位置
LOC[aij] = LOC[a11]+[3*(i-1)-1+j-i+1]*size
=LOC[a11]+[2(i-1)+j-1]*size
5.3.2、稀疏矩阵
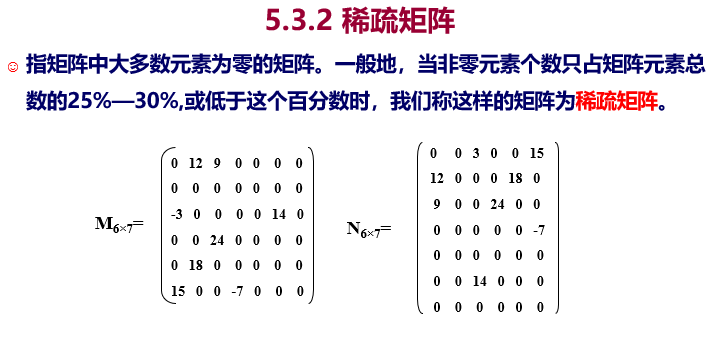
由于这种矩阵毫无规律可循,也就没有和之前几个矩阵一样的公式或函数表达了。
为此我们采用了存储坐标和元素值的做法——即 三元组表示法 。
至于为什么稀疏矩阵的定义是非零元素个数只占矩阵元素总数的25%—30%,或低于这个百分数,那是因为超过这个百分数太多三元组就不是压缩而是扩容了……
1、三元组表示法:
- 对于稀疏矩阵的压缩存储要求在存储非零元素的同时,还必须存储该非零元素在矩阵中所处的 行号 和 列号 。
- 我们将这种存储方法叫做稀疏矩阵的 三元组表示法。
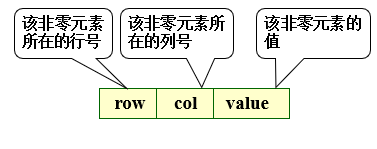
可以看到这时一个数组中的元素就对应了三个值,因此我们可以把它们整合一下做到结构体里面。
2、三元组表的类型定义:
1 |
|
3、稀疏矩阵的转置运算:
矩阵转置:指变换元素的位置,把位于(row,col)位置上的元素换到(col ,row)位置上,也就是说,把元素的行列互换,正常矩阵算法:
1 | void TransMatrix(ElementType source[m][n], ElementType dest[n][m]){ |
具体算法实现:
基于人类语言来说,我们肯定会更倾向于进行下面两个步骤快速得到结果:
- 将三元组表中所有元素进行 col 与 row 的调换。
- 对新得到的三元组表进行重新排序。
虽然步骤一较为便捷,但是问题出在步骤二上:它必然涉及大量的元素移动操作,极大地影响了算法效率。
所以教材中介绍的两种算法都属于一次成型:
1、序列递增转置法:
它是将 A 三元组表按列序依次放入 B 三元组表的,这样一来转置后得到的 B 三元组表是按照 行序排列 的。
1 | /*把矩阵A转置到B所指向的矩阵中去。矩阵用三元组表表示*/ |
2、一次定位转置法:
方法一中,我们为了匹配出对应位置,进行了两次循环,而这也大大增加了算法的时间复杂度。因此,为了简化算法,我们的方向就是减少循环次数。
这里我们想到了之前的 数组地址计算 ,通过地址计算,我们就可以减少一次循环。当然,为了计算的方便,有一些量必须提前得出。
☺设两个数组
**num[col]**:表示矩阵 A 中第 col 列中非零元个数
**position[col]**:指示矩阵 A 中第 col 列第一个非零元在 B 中位置(下标值)
再遵循如下的计算方式,得出具体位置:
① position[1] = 1
② position[col] = position[col - 1] + num[col - 1]
1 | /*基于矩阵的三元组表示,采用快速转置法,将矩阵A转置为B所指的矩阵*/ |
教材上也讲了,其实这是拿空间复杂度换了时间复杂度。
4、十字链表——稀疏矩阵的链式存储结构:
不需要怎么具体阐述,就记住是俩维度的链表,重要的是具体结构很特殊。
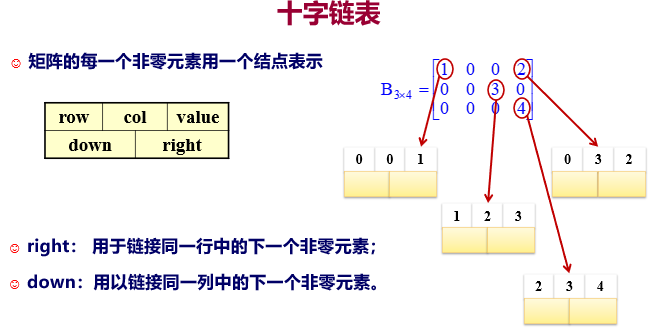
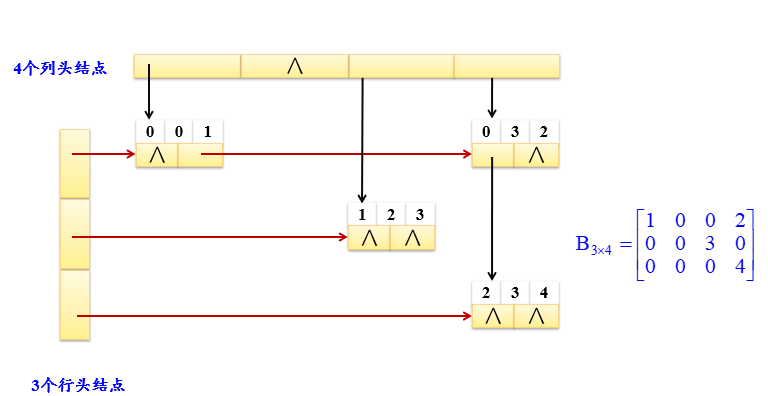
十字链表的结构类型定义
1 | typedef struct OLNode{ |
5.4、广义表
☺ 广义表 是线性表的推广,是有限个元素的序列,其逻辑结构表示法:
♫ GL = (d1,d2,d3,…,dn)
☺ 广义表中的di既可以是 单个元素,还可以是一个 广义表。
☺ GL是广义表的名字,通常用大写字母表示。
☺ n是广义表的 长度。
☺ 若 di是一个广义表,则称di是广义表GL的子表。
☺ 在GL中, d1是GL的表头,其余部分组成的表(d2,d3,…,dn)称为GL的表尾。
5.4.1、广义表的概念



5.4.2、广义表的两种储存结构:
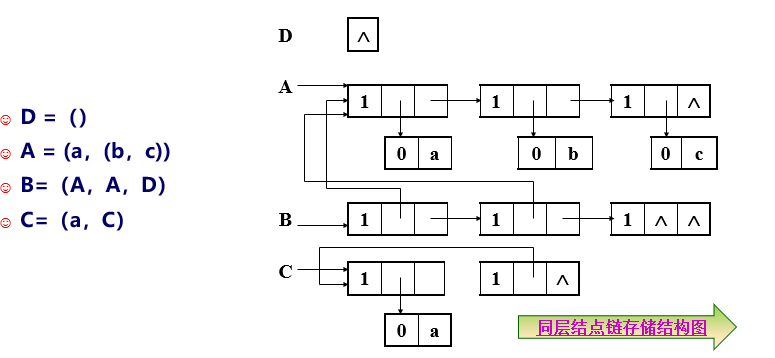
1 | typedef enum {ATOM, LIST} ElemTag; /*ATOM=0,表示原子;LIST=1,表示子表*/ |
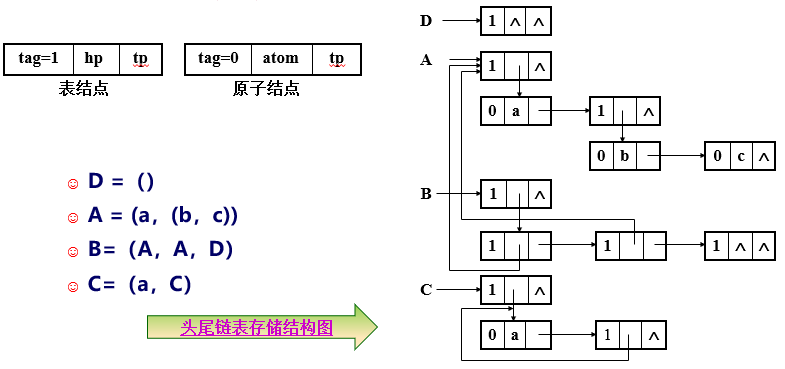
1 | typedef enum {ATOM, LIST} ElemTag; /*ATOM=0,表示原子;LIST=1,表示子表*/ |