132模式

发表于 | 更新于: | 分类于 |
字数统计: 684 字 | 阅读时长 ≈ 2 分钟

这道题主要涉及到了单调栈的运用，我还不是很熟悉这一类题型

题干:

给你一个整数数组 nums ，数组中共有 n 个整数。132 模式的子序列 由三个整数 nums[i]、nums[j] 和 nums[k] 组成，并同时满足：i < j < k 和 nums[i] < nums[k] < nums[j] 。

如果 nums 中存在 132 模式的子序列 ，返回 true ；否则，返回 false 。

进阶：很容易想到时间复杂度为 O(n^2) 的解决方案，你可以设计一个时间复杂度为 O(n logn) 或 O(n) 的解决方案吗？

示例 1：

输入：nums = [1,2,3,4]
输出：false
解释：序列中不存在 132 模式的子序列。
示例 2：

输入：nums = [3,1,4,2]
输出：true
解释：序列中有 1 个 132 模式的子序列： [1, 4, 2] 。
示例 3：

输入：nums = [-1,3,2,0]
输出：true
解释：序列中有 3 个 132 模式的的子序列：[-1, 3, 2]、[-1, 3, 0] 和 [-1, 2, 0] 。

提示：

  • n == nums.length
  • 1 <= n <= 104
  • -109 <= nums[i] <= 109

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/132-pattern

读完后第一反应是找一些方便判断的特征，找到对应的候选数字后不断进行维护。。。然后运行的时间复杂度是O（n^2）,而且在写代码时让人非常不舒服，过程过于繁杂且容易出错。

所以这里我们引入单调栈，即用栈存储数据，且栈内数据一定是单增（或单减），一旦遇到下一个数就立马用其与栈内元素比较，大于（或小于）的元素则全部出栈，最后将新的数压栈。

对于这道题，我们用单减的单调栈，即栈内元素中一定存在代表132模式中“3”的元素，而出栈元素用一个max变量维护，保证max对应132中“2”的候选元素中的最大值。此时，只要新的元素小于max，即可返回true（即新元素为132模式中代表“1”的元素）

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
bool find132pattern(int* nums, int numsSize){

  if(numsSize<3)

  return false;

  int stack[numsSize];

  int nu=0,max=-1000000001;

  stack[nu++]=nums[numsSize-1];

  for(int i=numsSize-2;i>=0;i--){

​    if(nums[i]<max)

​    return true;

​    for(int j=nu-1;j>=0;j--)

​    if(stack[j]<nums[i]){

​    nu--;

​    max=stack[j];

​    }

​    stack[nu++]=nums[i];

  }

  return false;

}

如下图解：

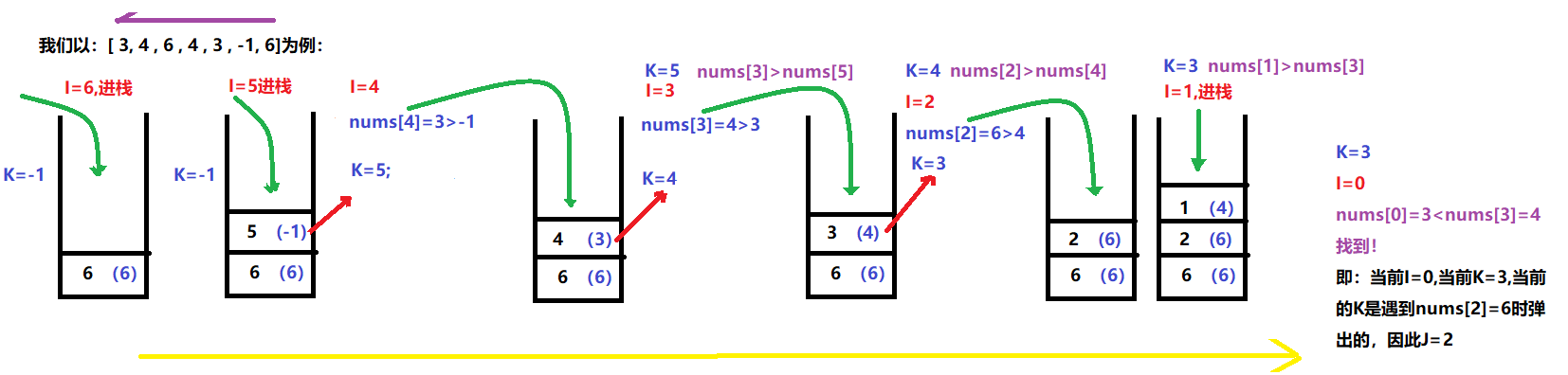
132模式

这里还有一篇关于单调栈的文章，写的很好，放个链接在这里：

https://blog.csdn.net/weixin_42784951/article/details/88963758?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522161659419116780262549524%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=161659419116780262549524&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v29-2-88963758.pc_search_result_cache&utm_term=%E5%8D%95%E8%B0%83%E6%A0%88